Computational complexity theory

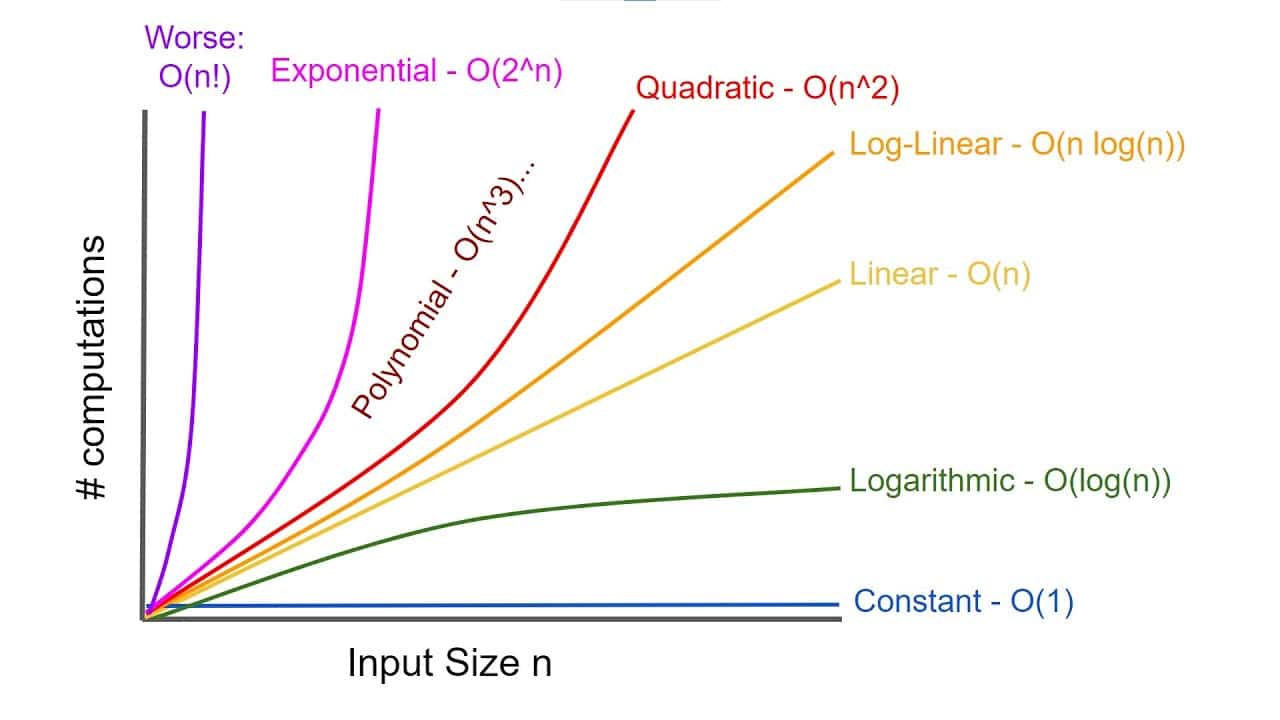
Computational complexity theory is a branch of mathematics and computer science concerned with the study of the resources, or complexity, required to solve problems. It seeks to identify and classify computational problems based on the amount of resources their solutions require. Its primary goals are to understand the inherent difficulty of computational problems and to determine the amount of resources (time and memory) needed to solve those problems.

Computational complexity theory has strong ties to theoretical computer science, as its main subject is the study of the resources necessary to execute an algorithm. It is also closely related to fields such as cryptography, cryptography, artificial intelligence, discrete mathematics, and so on.

Computational complexity theory encompasses a number of topics including algorithms, complexity classes, analysis of algorithms, algorithmic problems, reduction among problems, and so on. An algorithm is a step-by-step procedure meant to solve mathematical or computational problems. Complexity classes are collections of problems that have similar computational complexity. The analysis of algorithms is the process of determining the resources required to solve a given problem, while algorithmic problems are those which require a specific computational process in order for them to be solved. Reduction among problems is the process of solving a problem by transforming it into another problem that can be solved using existing algorithms.

Computational complexity theory provides key tools and ideas which can be used to design efficient algorithms and to analyze the amount of resources required to solve problems. It has had a lasting impact on the fields of mathematics, computer science, and cryptography.